The Monty Hall problem

[Retro]

Here's a great explanation of the Monty Hall problem with great graphics and clear dialog on the Fexl channel.

To view this content we will need your consent to set third party cookies.
For more detailed information, see our cookies page.

Accept third party cookies

If you want to read about it:

Monty Hall problem - Wikipedia

en.wikipedia.org

 

[Mars]

Don't have time to listen to it all now, but I have immediately found a flaw in the explanation: in the 100 doors example the 'skipped' door has a 99% chance of having the car behind it, while the gamer's original choice, door 1, still has its piddly 1% chance. Really?

I don't agree, and here is why: with all the doors having been eliminated, and only TWO doors left, the chance of the car being behind either of them is 50/50. NOT 99% vs 1%.

I shall definitely come to it later and watch it to the end, see what I think then.

 

[Retro]

Yeah, I agree, something doesn't compute there and it confused me. When that happens, it's usually because something doesn't make sense. Didn't want to say anything in the first post to avoid biasing readers. However, this is somehow proven mathematically so the Wikipedia article may help. I still wanna fully get my head around it before I accept it.

I think Veritasium also did a video on this, so I'll try to find it and post it here.

 

[Hitcore]

Here's a great explanation of the Monty Hall problem with great graphics and clear dialog on the Fexl channel.

To view this content we will need your consent to set third party cookies.
For more detailed information, see our cookies page.

Accept third party cookies

If you want to read about it:

Monty Hall problem - Wikipedia

en.wikipedia.org

With two doors left, there is a 50/50 shot, no matter how much they overcomplicate this. I'm the kind of person who can't be bothered with some TV show host's cheap mind tricks and I would just stick with the initially chosen door, I am stubborn like that. If I win a goat, I actually take the goat back home with me, I have a big garden and barn, he can live there. I will name the goat Dennis and I will love him. If I win the car, it will be of no use for me as I do not own a driver's license, and I will most likely end up selling the car, and will buy a goat, possibly the same goat from the show even, because I really like Dennis. Ergo: I always win. Mathematicians hate me.

 

[Retro]

Mathematicians hate me.

Haha I love that.

Thing is, it's been mathematically proven, allegedly. Normally when things like this don't quite make sense, I let it slide after thinking about it a bit. Gonna make an exception in this case though and make the extra effort to understand all the angles and come to a more informed conclusion. It still looks 50/50 to me too.

 

[Hitcore]

So picrelated is what's causing them to say: "ThErE aRe MoRe WiNNinG sCeNaRiOs WiTh sWiTcHiNg So MaThEmAtTiCaLLy tHiS iS pRoOf!!!!11one"



But if we look closely they are lumping together staying winning reveals into one (Door [x] or Door [x]). It may sound trivial but technically they are different scenarios. Individualize them on the silly chart and we get the same amount of wins as losses.
50/50.
I just broke the internet.

 

[Retro]

Ok, I've now looked at it properly, critically, I've also drunk the koolaid, and can confirm that the theory is right: you should switch every time to improve your odds to 2/3.

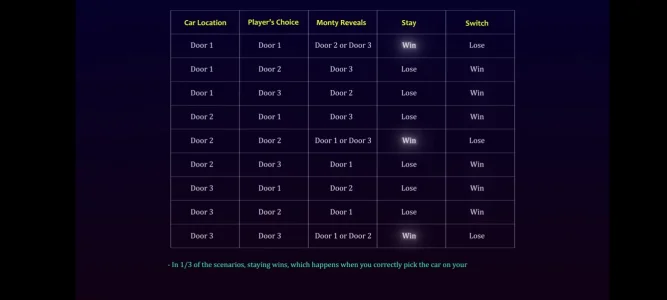
Without going through the whole explanation again, the core of it is that when you pick the initial door, you know nothing about what's behind any of the doors, making it 1/3 that you'll win the car. When Monty opens the door is when critical new information comes in that changes the odds: he will always open the door with the goat behind it since he knows where the car is. If he didn't know where the car is, then the probability would become 1/2 like people usually think initially as sometimes he would open the door with the car behind it, but that never happens. Therefore, when Monty opens the door, the 2/3 probability is concentrated in the unopened door. In the 100 door version, it becomes easier to see, since the 99% probability is now concentrated in that one remaining unopened door. Once you understand this, the whole thing falls into place.

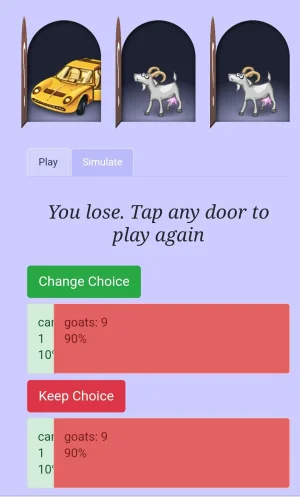
Here's a handy online simulator to demonstrate the game in action, proving the theory. I like the way it allows you to play with the various options, including simulation speed. I suggest setting the runs to 1000 and speed to instant for the clearest results.

Monty Hall Problem Online. Run the monty hall game and simulation , over and over to understand the probability of this problem.

Monty Hall Problem --a free graphical game and simulation to understand this probability problem.

www.mathwarehouse.com

Here's 4 Numberphile videos explaining it in various ways, which helped me to understand how this works.

In the first video, a nice lady, Lisa Goldberg, an adjunct professor in the Department of Statistics at University of California, Berkeley, explains it:

To view this content we will need your consent to set third party cookies.
For more detailed information, see our cookies page.

Accept third party cookies

In the second video, she explains it with some confusing squiggly math. It's basically the same video with the maths bits left in:

To view this content we will need your consent to set third party cookies.
For more detailed information, see our cookies page.

Accept third party cookies

In the third video, Brady Haran, the maker of these Numberphile videos, explains it in just 4 minutes in a clear, intuitive way:

To view this content we will need your consent to set third party cookies.
For more detailed information, see our cookies page.

Accept third party cookies

In the fourth video, Brady explains it in just 48 seconds! It's so efficient, love this.

To view this content we will need your consent to set third party cookies.
For more detailed information, see our cookies page.

Accept third party cookies

Finally, looking at these other videos and the simulator, I think the original video's explanation in my first post is too long at almost 20 minutes and I did notice that he repeated himself several times, which only causes confusion. It actually only takes 5 minutes to explain, a bit more with the squiggly math thrown in as a bonus.

 

[EGPRC]

What creates the disparity is the fact that the host is not revealing a door randomly but instead it is assumed as a rule that he knows the locations and purposely avoids to open both the player's chosen door and which contains the prize. He always removes doors until two are left, taking care of not removing any of those two.

That means that whenever the player starts failing, the host is inevitably indicating where the car is: in the only other option that he avoids to remove from the rest. With 100 doors, the player would pick wrong in 99 out of 100 attempts, on average, and as the prize is not allowed to be revealed anyway, in those 99 out of 100 times it will be in the other door that the host purposely left closed.

It's like if a second player came to play, he cheated by looking inside all the doors that the first did not pick, and took which preferred from them. In that way, it is obvious that the cheater will pick the winner as long as it is any of the 99 non-chosen ones, so 99% of the time.

 

[Retro]

Indeed, the fact that Monty knows where the car is and hence will never reveal it is the key to this.

Welcome to NerdZone Forums @EGPRC

 

[Hitcore]

I've watched every video, Retro, and I must say: that is really interesting. But... theory is nice 'n all, so I wanted to test it in practice. I went to the simulator:

Monty Hall Problem Online. Run the monty hall game and simulation , over and over to understand the probability of this problem.

Monty Hall Problem --a free graphical game and simulation to understand this probability problem.

www.mathwarehouse.com

It seems that no matter what I do, whether I decide to change or keep, 9 out of 10 times I get the goat.
To me it is clear now that the universe wants me to fulfill my one and true purpose in life: to become a goat herder.

 

[Retro]

Here's something people may not realise: selecting one door and then switching when Monty opens a door is actually equivalent to just opening two doors yourself without all that faffing! It's the same 2/3 probability of winning, but with less drama and hence entertainment value.

If I'd gone on the show, I'd be the smartass who points this out, lol.

 

[Mars]

Agreed, exactly my thoughts when i first posted back in March, it is a whole lot of theatrics; at the end, it all boils down to two doors: the door the contestant chose, and the one door left closed. 50/50.

 

[Retro]

50/50.

Sorry, no, it's still a 2/3 probability like it always was, the program just went the long way round to make good TV.

 

[Mars]

At the end of the day the contestant is faced with two closed doors. One door hides a car, the other hides a goat; so, if we look at it from from the contestant's point of view, it is a 50/50.
Unless I am missing something it looks 50/50 to me.

 

[EGPRC]

At the end of the day the contestant is faced with two closed doors. One door hides a car, the other hides a goat; so, if we look at it from from the contestant's point of view, it is a 50/50.
Unless I am missing something it looks 50/50 to me.

You can distinguish between the two remaining doors: one was selected by you and the other was left by the host. To make it clearer, when you first make a choice, put a label with your name on it. Then, after the host reveals a goat from the rest, he also puts his name "Monty" on the other that he avoids to open. In that way, you will always face two doors, but does that mean that the one labeled with your name will hide the car with the same frequency as which is labeled with Monty's name? One thing has nothing to do with the other.

As you choose randomly from three, you only manage to put your name on which has the car in 1 out of 3 attempts, on average. And as he is never allowed to reveal the car anyway, he is who uses his knowledge to leave it hidden in the one that marks as "Monty" (the switching door) in the 2 out of 3 times that you start failing.

In other words, the fact that always one of you two manage to complete the work of keeping the car hidden does not mean that you are as good as the host at doing it.

 

[Mars]

@EGPRC, thanks, yes, I know how the game works.
My point is simple: at the end of the day, the contestant is faced with two doors, only two not three. One of which hides the car, only two choices. Hence 50/50. Anyway, that's how I see it.

 

[Geffers]

Numbers can be confusing but one has to take in to consideration that you may have chosen the car correctly in the first place so your second 'change your mind' option may be to actually LOSE the car and win the goat.

 

[Retro]

Oh yes, there has to be jeopardy, or the competition would be pointless!

It's funny how hard it is to see that switching gives you a 2/3 probability of winning it when choosing two doors is done in this roundabout way rather than simply opening a random two to start with. It took my a while and lots of concentration on different videos to properly get it.

 

[EGPRC]

@EGPRC, thanks, yes, I know how the game works.
My point is simple: at the end of the day, the contestant is faced with two doors, only two not three. One of which hides the car, only two choices. Hence 50/50. Anyway, that's how I see it.

You are only focusing on the fact that there are two doors, but what does make you think that the car is equally likely to be behind which you chose than behind the other left by the host? Because for it to be 1/2 chance you have to also be sure that each will yield the prize with the same frequency. In general, uniform distributions are not the only ones that exist, so you cannot always assume that each option will have the same amount of probability.

 

[Geffers]

Pondered this more during Sunday and my conclusion is that is is a 50/50 chance and here is why I think that way.

Three choices to start but in fact the first choice is totally irrelevant, A, B or C doesn't matter, matters not whether your choice is the car or the goat as at that point it is unknown. Monty will then remove one door containing a goat, leaving two choices and one will be the car.

Your 50/50 choice is door one of two or door two of two. The first choice actually confuses the issue but does not enter into the puzzle at all.

Geffers

 

[Retro]

@Geffers It really is 2/3 not 50:50 as it's been mathematically proven. I know it's confusing to get one's head around it, it took me long enough too and I also thought 50:50 initially, but it's worth the effort. I made the post below with a comprehensive explanation of how this works which will clarify it. There's quite a lot to read there, so I recommend fortifying yourself with a cup of tea first.

Some people found the last video, just 48 seconds long, was enough to get it, so perhaps start with that.

The Monty Hall problem

Here's a great explanation of the Monty Hall problem with great graphics and clear dialog on the Fexl channel. If you want to read about it: https://en.wikipedia.org/wiki/Monty_Hall_problem

nerdzone.uk

Also have a look at this post afterwards:

The Monty Hall problem

Here's a great explanation of the Monty Hall problem with great graphics and clear dialog on the Fexl channel. If you want to read about it: https://en.wikipedia.org/wiki/Monty_Hall_problem

nerdzone.uk

 

[Mars]

Pondered this more during Sunday and my conclusion is that is is a 50/50 chance and her is why I think that way.

Three choices to start but in fact the first choice is totally irrelevant, A, B or C doesn't matter, matters not whether your choice is the car o the goat as at that point it is unknown. Monty will then remove one door containing a goat, leaving two choices and one will be the car.

Your 50/50 choice is door one of two or door two of two. The first choice actually confuses the issue but does not enter into the puzzle at all.

Geffers

I agree, for me it is clearly 50/50. Even looking at the example of 100 doors, in the final analysis, the contestant is faced with two, and only two, choices. One out of Two.
No matter how mathematicians try to confuse/complicate the issue, they can talk until they are blue in the face; it will always remain One of Two.
A maths teacher once told me that it is a known fact that mathematicians sometimes trip over their own toes, over complicating issues.

 

[Retro]

@Mars seriously, no. Have a look at my post above yours and the explanations it points to.

Remember, it's been mathematically PROVEN so the only question you should be asking now is "how can I understand it?" Same goes for Geffers or anyone else who insists on 50:50. Really, it's as black and white as that, not an opinion.

 

[Mars]

Yes, I did look at the explanation, and I do not agree that after Monty opens his goaty door the probability suddenly becomes 2/3.
Why 2/3?
Think about it: once he opened his dud door, there are two closed doors left, so the probability of the car being behind either one of the remaining closed doors is 1 of 2, not 2 of 3: there is no third closed door any longer!

It cannot be 2 of 3, because there are only two closed doors, not three.

 

[Retro]

What about the fact that it's been proven by mathematicians? Is that something to be debated or ignored, or for you to try and understand how it works?